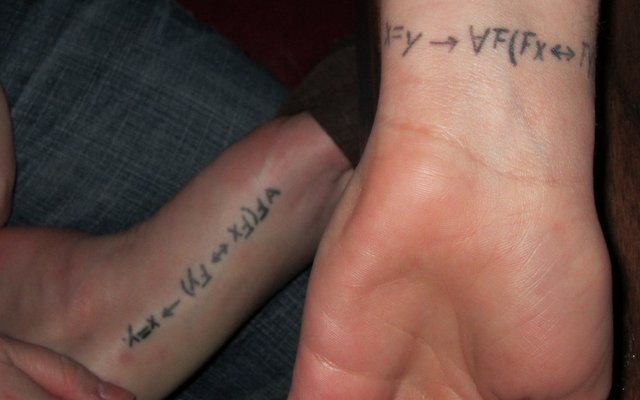
I love philosophy majors. The best of them almost always develop a nerdy and warped sense of humor – and I mean that in the best way. 🙂
These two young ladies, recent alumnas of our department, decided to get complementary tattoos. (Sober, they swear!)
In each case, the tattoo artist left off the two initial universal quantifiers: AxAy (I can’t find the symbol codes for the upside down A representing the universal quantifier – so please imagine those A’s upside down.) They would read: For any x whatsoever and for any y whatsoever…
Now to the tattoos. “F” is supposed to be, either a predicate or a property. On the right tattoo (wrist) the right, closing parentheses is just out of view.
One of the tattoos says something nearly all philosophers agree is true (a rarity!) while the other is held to be false by many. Here’s your homework, dear reader: Which, and why? (Hint #1: one is called the Identity of Indiscernibles, and the others is the Indiscenibility of Identicals. Hint #2: I’ve preached quite a lot about the true on on this blog.)
While you’re thinking, the best and funniest song ever written about tattoos.
Helpful little reminder there at the end. 🙂
Also, there’s the Live at Leeds version, with a funky recent video added to it.

Since no one else has jumped in on this one, most philosophers think the formula on the right wrist is true, the one on the left false. The right one says that if x and y are one and the same thing, then any predicate which applies to one must apply to the other and vice versa. The left one says that if any x and y are such as to be indistinguishable (any predicate that applies to the one applies to the other and vice versa) then they (“they”) are one and the same.
The famous Christian philosopher Leibniz affirmed both. But many hold that the second wrongly rules out the possibility completely indistinguishable but numerically different things.
I’ve posted on “Leibniz’s Law” (the first one – the one on the right wrist. I think there is a necessary and self-evident truth there, but I wouldn’t put it in terms of predicates. As to the other, I don’t think it is self-evident at all. Whether it is false, I’m agnostic about.
Hi Eluros,
I don’t know how to interpret this:
~(VF(FxFy)->x=y)
F_ is supposed to be a one-place predicate (e.g. Fx means that x is F. I don’t know what is meant by FxFy – we need a truth-functional operator connecting those…
WARNING! SPOILERS!
So, it’s been a few years since my formal logic classes, but how’d I do?
@1. ~(VF(FxFy)->x=y) (Denied Premise)
@2. ~(~(VF(FxFy))v(x=y)) (1 Conditional)
@3. ~~(VF(FxFy))^~(x=y) (2 DeMorgans, I think?)
@4. (VF(FxFy))^~(x=y) (3, DN)
5. (VF(FxFy)) (4)
6. ~(x=y) (4)
@7. AxAy (5)
8a. Ax
8b. ~Ax
9a. Ay
9b. ~Ay
@1. ~((x=y)->VF(FxFy)) (Denied Premise)
@2. ~(~(x=y)v(VF(FxFy))) (1 Conditional)
@3. (~~(x=y)^~(VF(FxFy))) (2 DeMorgans, I think)
@4. (x=y)^~(VF(FxFy)) (3 DN)
5. x=y (4)
@6. ~(VF(FxFy)) (4)
@7. EF~(FxFy) (6)
@8. ~(FaFb) (7)
9a. Fa
9b. ~Fa
10a. ~Fb (x9a, 5)
10b. Fb (x9b, 5)
Thus, ((x=y)->VF(FxFy)) is true, while (VF(FxFy)->x=y) is false.
Any mistakes? Did I do that correctly?
Comments are closed.